Anomaly Detection
Definition of Time Series
Definition
A time series (instance) is a sequence of real numbers:
A time series model is a sequence of random variables:
Examples
-
Let be independent standard-normally distributed. Then the time series model with is called standard-white noise.
-
Let be a real number, then is a time series model with constant expectation
-
Let be real numbers, then is a time series with affine-linear expectations
Remark
For a given time series and model we get a probability for the occurencye of :
In case the model has a joint probability density function we get a probability density for the time series :
## Numerical Simulation of Examples
import random
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = (9.0, 3.0)
eps = lambda : random.normalvariate(0,1)
Y1 = [ eps() for i in range(100)]
Y2 = [ eps() + 5 for i in range(100)]
Y3 = [ eps() - 3 + 0.2 * i for i in range(100) ]
plt.title("Time series samples")
plt.plot(Y1, 'r.', label="Standard white noise")
plt.plot(Y2, 'g.', label="Normal noise with mean")
plt.plot(Y3, 'b.', label="Normal noise with mean and drift")
plt.legend(loc = "upper left")
plt.show()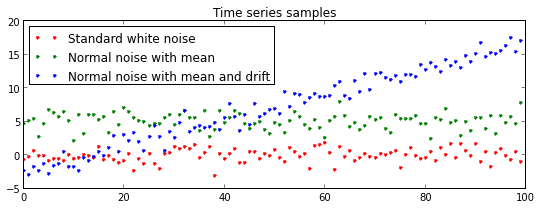
Parameter Estimation
Definition Let for be a family of time series models, and let be a time series instance. We write and for and .
The maximum likelihood estimator (MLE) (cf. wikipedia) for in is defined as
In case the model has a density function we set
Note that the maximum likelyhood estimater does not need to exists, nor is it unique if it exists.
Example
- Let and with model , then
The value is maximal if the sum of squares is mininmal. Threfore
- Similarly, for the model and the MLE minimizes the following sum of squares
This problem is quivalent to Linear Regression.
# Linear Regression Example adapted from
# http://glowingpython.blogspot.de/2012/03/linear-regression-with-numpy.html
import numpy as np
from scipy import stats
y = [19, 20, 20.5, 21.5, 22, 23, 23, 25.5, 24]
T = np.arange(0,9)
m, b, _,_,_ = stats.linregress(T,y)
line = b + m * T
const = np.mean(y) + 0 * T
plt.title("MLE Estimators")
plt.plot(T,y,'ro', T, const, 'g-', T,line,'b-')
plt.legend(("Samples", "Mean", "Regression line"), loc="upper left")
plt.show()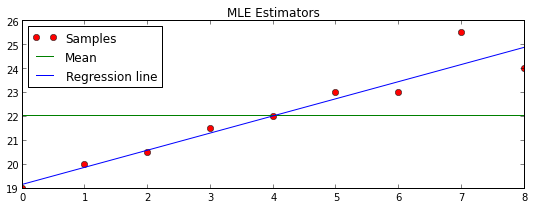
Hypothesis Testing
Let and be two families of models, indexed by and a time series instance. We consider the following statements:
- The sample was drawn from a model in
- The sample was drawn from a model in
In order to decide between those statements, we consider their likelihood ratio.
Definition
We define the Likelihood ratio to be
or, in the continues case
We define the Log-likelihood ratio as .
For a given confidence level we accept the Hypythesis if .
Example
Take , a time series and . To test the hypothesis
- : The instance was drawn from
- : The instance was drawn from
we calculate the likelihood ratios as:
where is the average of , the variable is half the distance between and and is the sample mean. For the second step we used the following simple identity:
Note, that if . And if , i.e. is closer to than to .
We accept the Hypothesis if , which is equivalent to:
# Numerical Hypothesis Test Example
from scipy.stats import norm
# Model Parameters
b0 = 0
b1 = 5
alpha = 10
def normal_density(b):
return lambda y : norm.pdf(loc=b,scale=1,x=y)
# probability density functions
p0 = normal_density(b0)
p1 = normal_density(b1)
plt.title("Probability Density Functions")
grid = np.linspace(-5,10,100)
plt.plot(grid,map(p0, grid))
plt.plot(grid,map(p1, grid))
plt.show()
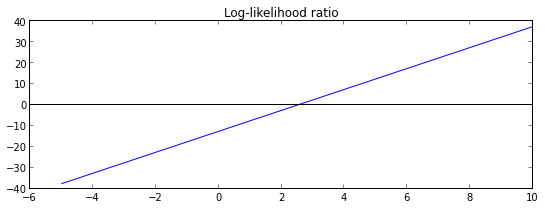
# Log likelihood ratio (for single sample)
l = lambda y : np.log(p1(y) / p0(y))
plt.plot(grid,map(l, grid))
plt.title("Log-likelihood ratio")
plt.axhline(color = 'black')
plt.show()
b = 1. / 2 * (b0 + b1)
delta = 1. / 2 * (b1 - b0)
l2 = lambda x : 2*delta*(x - b)
print "l2 == l ? " + str(np.max(map(lambda x: l(x) - l2(x), grid)) < 10**-7)
# Time series instance
Y = [0.1,0.3,.4,.1,-.1,-0.3,0.3,-0.2,2,-1,5.2]*1
random.shuffle(Y)
plt.title("Time Series Instance")
plt.plot(Y, 'o')
plt.axhline(b0)
plt.axhline(b1)
plt.show()
log_lhr = lambda Y : sum(l2(y) for y in Y)
from IPython.display import Latex
print "Hypothesis H_1 accepted: {}".format(log_lhr(Y) > np.log(alpha))
Latex("Log likelihood ratio $$\lambda={}$$ for plotted time series Y".format(log_lhr(Y)))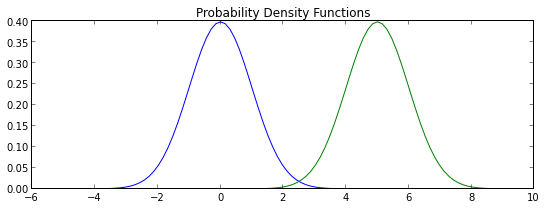
l2 == l ? True
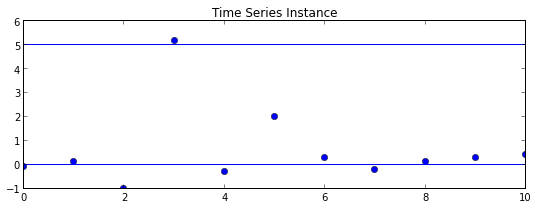
Hypothesis H_1 accepted: False
Log likelihood ratio for plotted time series Y
Test for changes in mean
For given we consider the hypotheses:
-
: Constant mean model
-
: Change in mean at a time :
For an instance we calculate the log-likelihood ration to be and using the notation from the last example we get
We introduce the notation so that we can write
The total log likelihood ratio is computed by explicit maximization:
Note, that , since .
log_lhr_k = lambda k, Y : 2 * delta * sum(y - b for y in Y[k+1:])
log_lhr_max = lambda Y : max( log_lhr_k(k,Y) for k in range(len(Y)))
Y = [0.1,0.3,.4,.1,-.1,-0.3,0.3,-0.2,2,-1,5.2,5,6,7,4,5]
ax = plt.axes()
ax.set_title("Time Series, Model-expectations and log-likelihood ratio")
ax.plot(Y, 'o')
ax.axhline(b0)
ax.axhline(b1)
ax2 = ax.twinx()
ax2.plot([log_lhr_k(k,Y) for k in range(len(Y))], 'y--')
plt.show()
Latex("$$\lambda = \max \lambda_k = {} $$".format(log_lhr_max(Y)))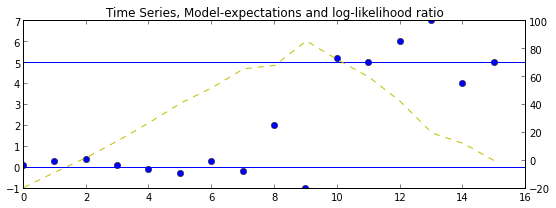
Online Variant
It turns out, that there is a simple recursion, which allows us to compute the likelyhood ratio for an instance of length from the knowledge of for the instance of length .
Indeed, we have Note, that .
The minimum-term we have
In case we have and in case
Since we always have , we get the total recursion:
Set then we get the recursion:
which is known as the CUSUM method.
log_lhr_T = lambda T: log_lhr_max(Y[:T])
# plt.plot([log_lhr_max(Y[:T]) for T in range(1,len(Y))])
def log_lhr_rec(T):
if T == 0: return 0
return max(0,log_lhr_rec(T-1) + 2 * delta * (Y[T] - b))
def log_lhr_iter(Y):
l = 0
for y in Y:
l = max(0, l + 2 * delta * (y - b))
yield l
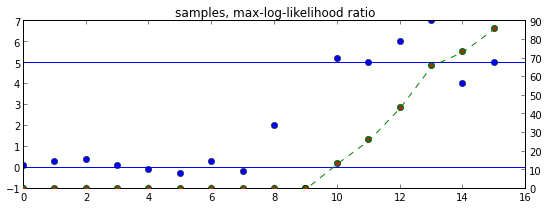
ax = plt.axes()
ax.set_title("samples, max-log-likelihood ratio")
ax.plot(Y, 'o')
ax.axhline(b0)
ax.axhline(b1)
ax2 = ax.twinx()
ax2.plot([log_lhr_max(Y[:T+1]) for T in range(len(Y))], 'go')
ax2.plot([log_lhr_rec(T) for T in range(0,len(Y))], 'r.')
ax2.plot(list(log_lhr_iter(Y)), 'g--')